坐标变换
基本定义
坐标变换这种方法在电网络、电力电子、电机建模与控制等很多领域都有应用,本文章以三相永磁同步电机为背景,主要讨论三相与两相间的转化
对于三相永磁同步电机而言,定子绕组可以等效为a,b,c三相绕组,假设这三相绕组的方向如img1所示
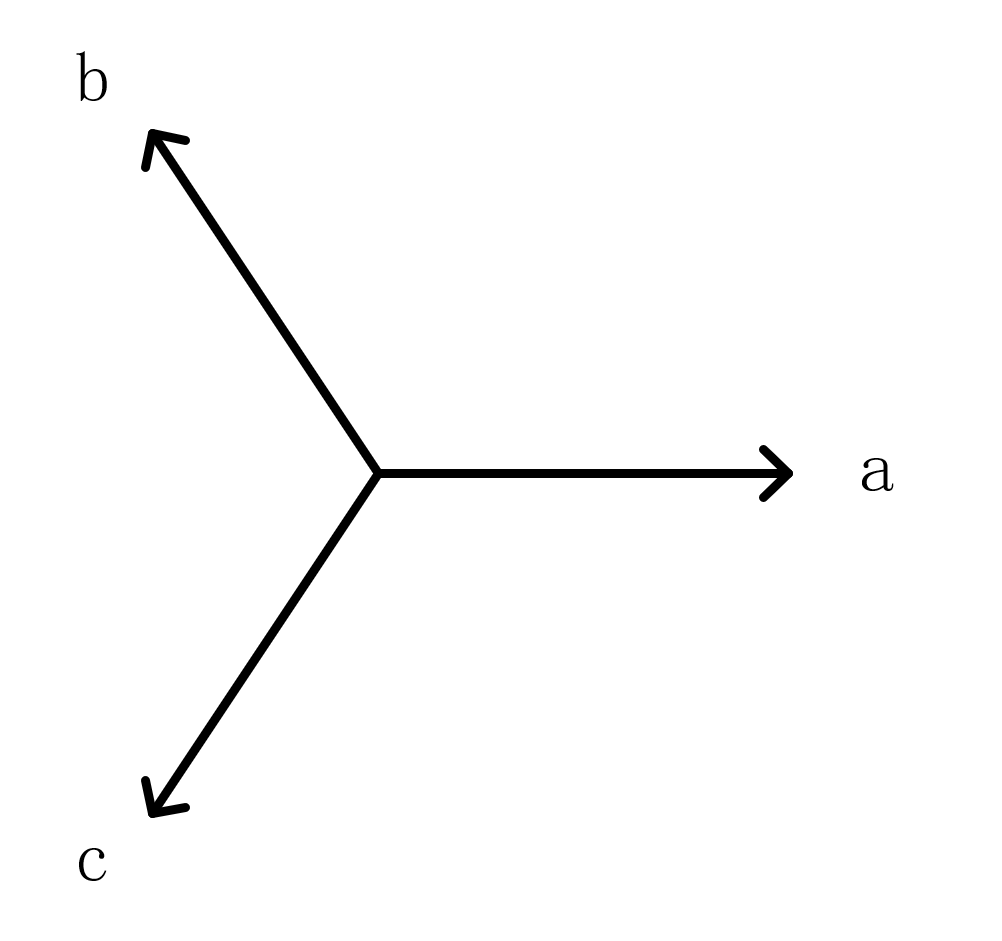
对于这三相绕组的任意一个物理量,比如电流,定义
$$
\begin{equation}
\boldsymbol{i_a}=i_a\boldsymbol{a},\boldsymbol{i_b}=i_b\boldsymbol{b},\boldsymbol{i_c}=i_c\boldsymbol{c}
\end{equation}
$$
需要注意的是,这里的$i_a,i_b,i_c$代表的是电流的大小,并且代表的是瞬态过程
恒相幅值变换
定义综合矢量$\boldsymbol{i}=k(\boldsymbol{i_a}+\boldsymbol{i_b}+\boldsymbol{i_c})$,这里的k是一个待定的系数
由于是恒相幅值变换,我们的目标是在稳态过程下,综合矢量的幅值等于a,b,c三相的幅值
本文先通过瞬态过程的推导得出公式,因为稳态过程就是瞬态过程的一个特例,所以可以直接代入公式,解得k的值
瞬态过程
要计算综合矢量的幅值,可以建立x-y坐标系,假设如图img2所示
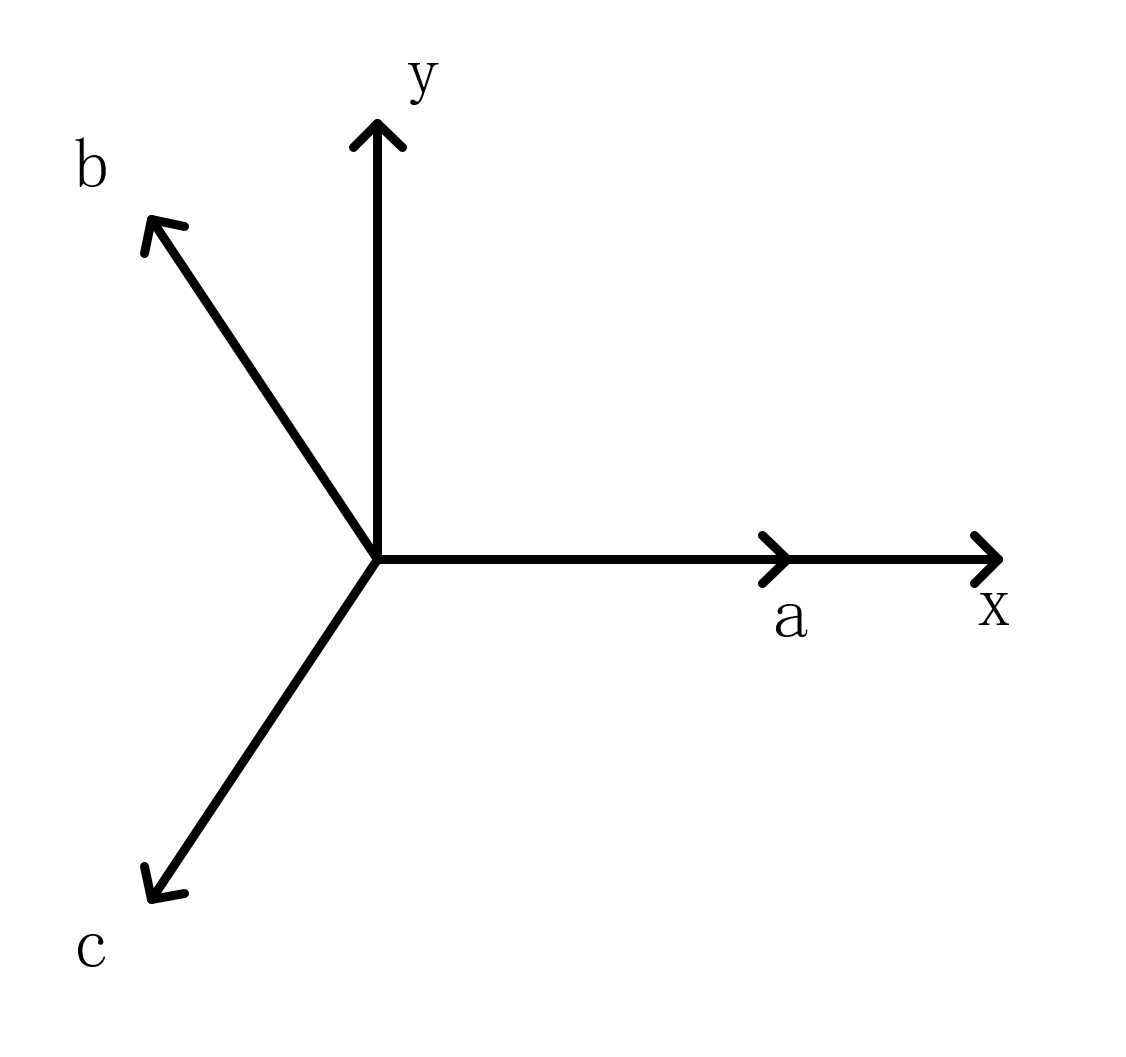
容易得到
$$
\begin{cases}
i_x=k(i_a-\frac{1}{2}i_b-\frac{1}{2}i_c) \\
i_y=k(\frac{\sqrt{3}}{2}i_b-\frac{\sqrt{3}}{2}i_c)
\end{cases} \\
$$
$$
\begin{equation}
i=|\boldsymbol{i}|=k\sqrt{i_x^2+i_y^2}=k\sqrt{\frac{1}{2}\sum\limits_{cyc}(i_a-i_b)^2}(1)
\end{equation}
$$
稳态过程
对于稳态过程,可以假设三相是相位分别相差$\frac{2}{3}\pi$,且幅值完全相同的正弦波,即
$$
\begin{cases}
i_a=I_m\cos(\omega t) \\
i_b=I_m\cos(\omega t-\frac{2}{3}\pi) \\
i_c=I_m\cos(\omega t+\frac{2}{3}\pi)
\end{cases}
$$
将上述三个式子代入公式(1),可以得到
$$
\begin{align}
i&=k\sqrt{\frac{1}{2}\sum\limits_{cyc}(I_m\cos\omega t-I_m\cos(\omega t-\frac{2}{3}\pi))^2} \\
&=k\sqrt{\frac{1}{2}I_m^2\sum\limits_{cyc}(-2\sin(\omega t-\frac{1}{3}\pi)\sin\frac{\pi}{3})^2} \\
&=k\sqrt{\frac{1}{2}I_m^2\sum\limits_{cyc}3\sin^2(\omega t-\frac{\pi}{3})} \\
&=k\sqrt{\frac{3}{2}I_m^2\sum\limits_{cyc}\frac{1-cos(2\omega t-\frac{2}{3}\pi)}{2}} \\
&=k\sqrt{\frac{9}{4}I_m^2} \\
&=\frac{3}{2}kI_m
\end{align}
$$
因此,如果要使变换前后幅值相等,应该令$k=\frac{2}{3}$
坐标变换
在得出了坐标变换的系数之后,就要对物理量进行坐标变换了,在叙述坐标变换的公式之前,应该先清楚坐标变换的目的
在三相永磁同步电机中,如果直接对a,b,c三相进行控制,将会非常复杂,因为a,b,c三相之间会互相耦合,也就是互感不为零,这将给控制带来麻烦
为此,我们希望先将a,b,c三相通过坐标变换变成两相,对两相进行控制,控制完成后再进行逆变换生成对应的三相控制量
具体的部分可参看【永磁同步电机】
坐标变换的类型主要有$abc-\alpha\beta 0,abc-dq0,abc-d_cq_c0$这么三种,具体定义参见下文,明白一种之后很容易就能举一反三,这里只给出$abc-\alpha\beta 0,abc-dq0$的公式
$abc-\alpha\beta 0$
a,b,c是电机等效绕组的方向,$\alpha$方向与a轴重合,$\beta$方向超前$\alpha$方向90度,如图img3所示
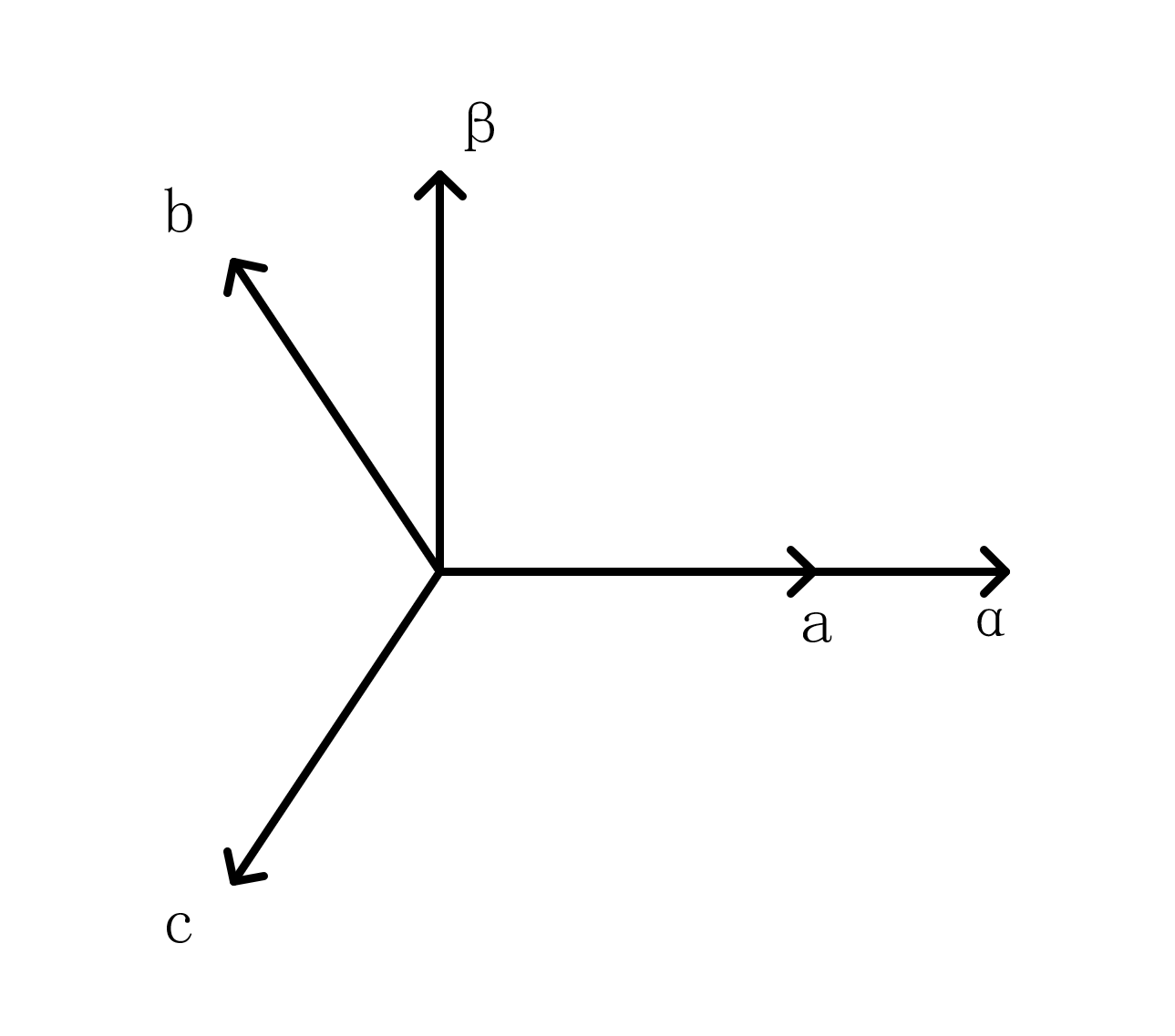
其实这里的$\alpha\beta$坐标与上面计算$|\boldsymbol{i}|$时用的x,y坐标是一样的,所以有
$$
\begin{cases}
i_\alpha=i_a-\frac{1}{2}i_b-\frac{1}{2}i_c \\
i_\beta=\frac{\sqrt{3}}{2}i_b-\frac{\sqrt{3}}{2}i_c
\end{cases}
$$
这样我们能通过abc坐标系,算出$i_\alpha,i_\beta$的值,但是反过来却不成立
如果$i_\alpha,i_\beta$的值确立,那么综合矢量就确定了,假设有一组$i_a,i_b,i_c$使得$\boldsymbol{i}=\frac{2}{3}(i_a\boldsymbol{a}+i_b\boldsymbol{b}+i_c\boldsymbol{c})$成立
由于$\boldsymbol{a}+\boldsymbol{b}+\boldsymbol{c}=0$,$i_a+const,i_b+const,i_c+const$都是满足条件的值,这样就有无数组解,其中const是任意实数,因此还需要一条方程约束
这里先给出方程,再证明为什么给出了这条方程,就能够完全确定$i_a,i_b,i_c$,方程如下
$$
\begin{equation}
i_0=\frac{1}{3}(i_a+i_b+i_c)
\end{equation}
$$
证明如下,上面说了,$i_\alpha,i_\beta$给定之后,综合矢量就完全确定了,作综合矢量关于$a,b,c$三轴的投影,并记为$i_a’,i_b’,i_c’$
$$
\begin{align}
i_a’&=\boldsymbol{i}\cdot \boldsymbol{a} \\
&=\frac{2}{3}(i_a-\frac{1}{2}i_b-\frac{1}{2}i_c)
\end{align}
$$
b,c相同理可得
$$
i_b’=\frac{2}{3}(i_b-\frac{1}{2}i_c-\frac{1}{2}i_a)
$$
$$
i_c’=\frac{2}{3}(i_c-\frac{1}{2}i_a-\frac{1}{2}i_b)
$$
可以发现$i_a=i_a’+i_0,i_b=i_b’+i_0,i_c=i_c’+i_0$
这就是说,只要再给定$i_0$,就可以完全推得$i_a,i_b,i_c$
这个过程用矩阵表示如下
$$
\begin{bmatrix}
i_\alpha \\
i_\beta \\
i_0
\end{bmatrix}=\frac{2}{3}
\begin{bmatrix}
1 & -\frac{1}{2} & -\frac{1}{2} \\
0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{bmatrix}
\begin{bmatrix}
i_a \\
i_b \\
i_c
\end{bmatrix}
$$
定义
$$
\begin{equation}
\boldsymbol{C}=\frac{2}{3}
\begin{bmatrix}
1 & -\frac{1}{2} & -\frac{1}{2} \\
0 & \frac{\sqrt{3}}{2} & -\frac{\sqrt{3}}{2} \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{bmatrix}
\end{equation}
$$
这里的$\boldsymbol{C}$就是变换矩阵,可以算得$|\boldsymbol{C}|\not ={0}$,故$\boldsymbol{C}$存在逆矩阵
逆矩阵可以通过纯粹的数学运算得出,也可以通过上述的物理意义得到
$$
\begin{equation}
\boldsymbol{C}^{-1}=
\begin{bmatrix}
1 & 0 & 1 \\
-\frac{1}{2} & \frac{\sqrt{3}}{2} & 1 \\
-\frac{1}{2} & -\frac{\sqrt{3}}{2} & 1
\end{bmatrix}
\end{equation}
$$
这样$abc-\alpha\beta 0$的正逆变换就都得到了
$abc-dq0$
d,q轴的定义是以转子转速$\omega$旋转的坐标系,设$\theta$是d轴与q轴的夹角,如img4所示
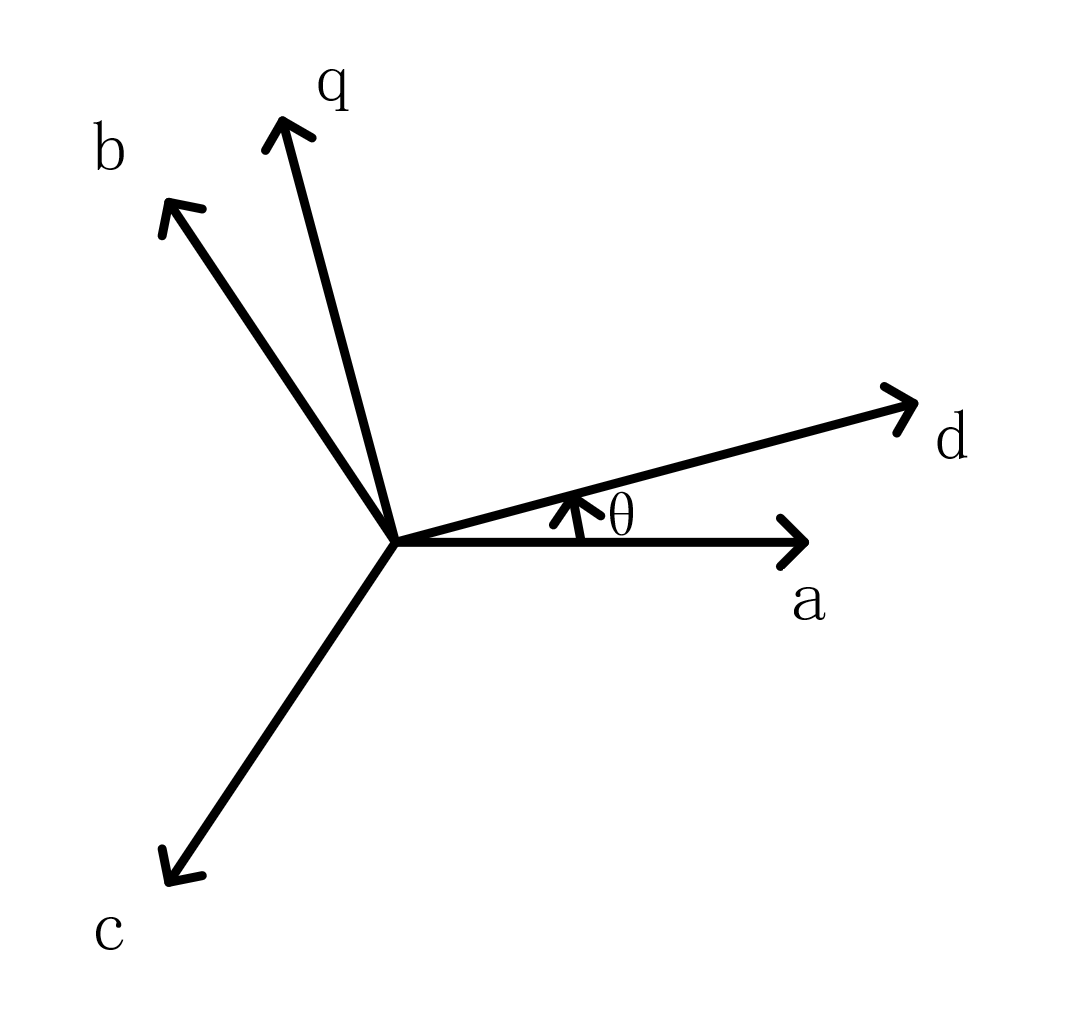
这里的坐标变换与$\alpha\beta 0$的坐标变换完全类似,可以根据物理含义直接给出
$$
\boldsymbol{C}=\frac{2}{3}
\begin{bmatrix}
\cos\theta & \cos(\theta-\frac{2}{3}\pi) & \cos(\theta+\frac{2}{3}\pi) \\
-\sin\theta & -\sin(\theta-\frac{2}{3}\pi) & -\sin(\theta+\frac{2}{3}\pi) \\
\frac{1}{2} & \frac{1}{2} & \frac{1}{2}
\end{bmatrix}
$$
$$
\boldsymbol{C}^{-1}=
\begin{bmatrix}
\cos\theta & -\sin\theta & 1 \\
\cos(\theta-\frac{2}{3}\pi) & -\sin(\theta-\frac{2}{3}\pi) & 1 \\
\cos(\theta+\frac{2}{3}\pi) & -\sin(\theta+\frac{2}{3}\pi) & 1
\end{bmatrix}
$$
$abc-d_cq_c0$
$d_c,q_c$轴是以同步速旋转的坐标系,在方程上与$abc-dq0$是完全一样的,只不过$\frac{d\theta}{dt}=\omega_c$为同步速而已