SVPWM

简介

SVPWM(Space Vector Pulse Width Modulation)，即电压空间矢量调制，是一种PWM生成方法，其作用是在主电路中生成给定的电压信号，而不是电机控制方法，这里需要与电机矢量控制做一个区分。

SVPWM给定的是目标电压矢量，输出的是六个PWM波，这六个PWM波控制IGBT的通断，在主电路中生成三相PWM，三相PWM的基波合成起来就是目标电压矢量。

基本原理

假设电机内部绕组接法为星形接法，以如下图所示的IGBT逆变器为例来进行说明

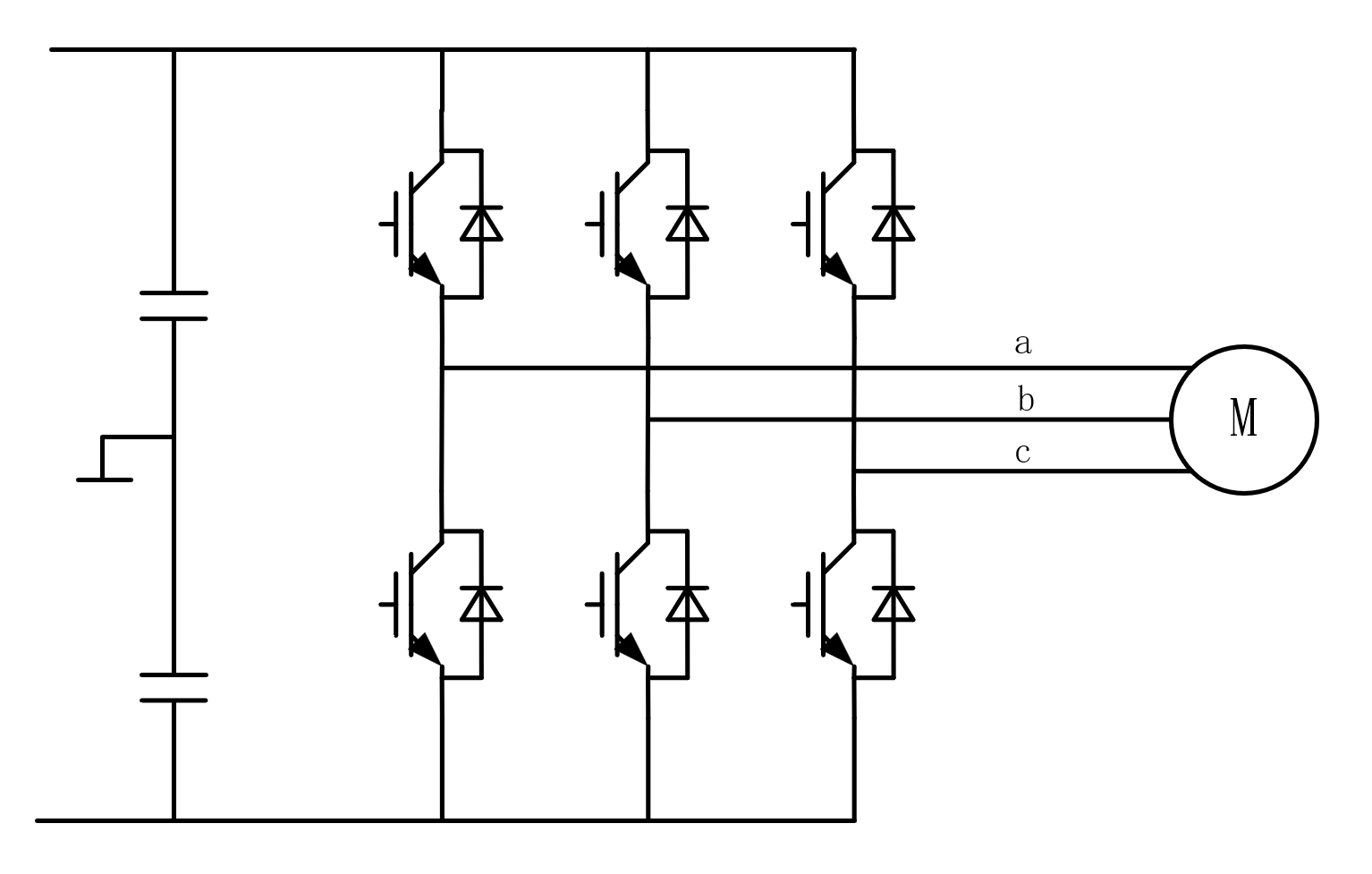
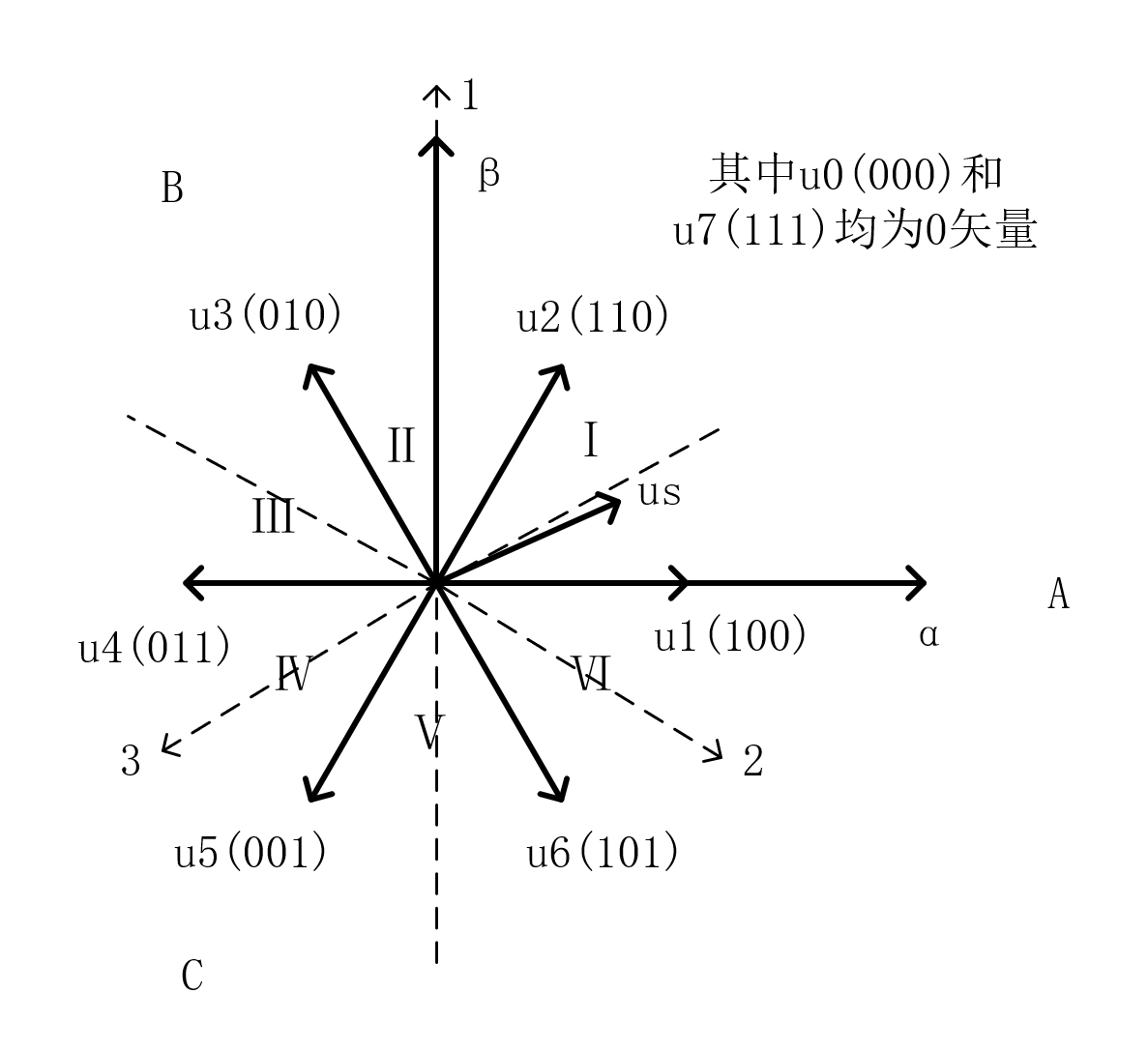
设$S_A=1$代表A相上管通，$S_A=0$代表A相下管通，$S_B,S_C$类似设定，则可以得到SVPWM的基本电压矢量为下图$u_0 ~ u_7$所示

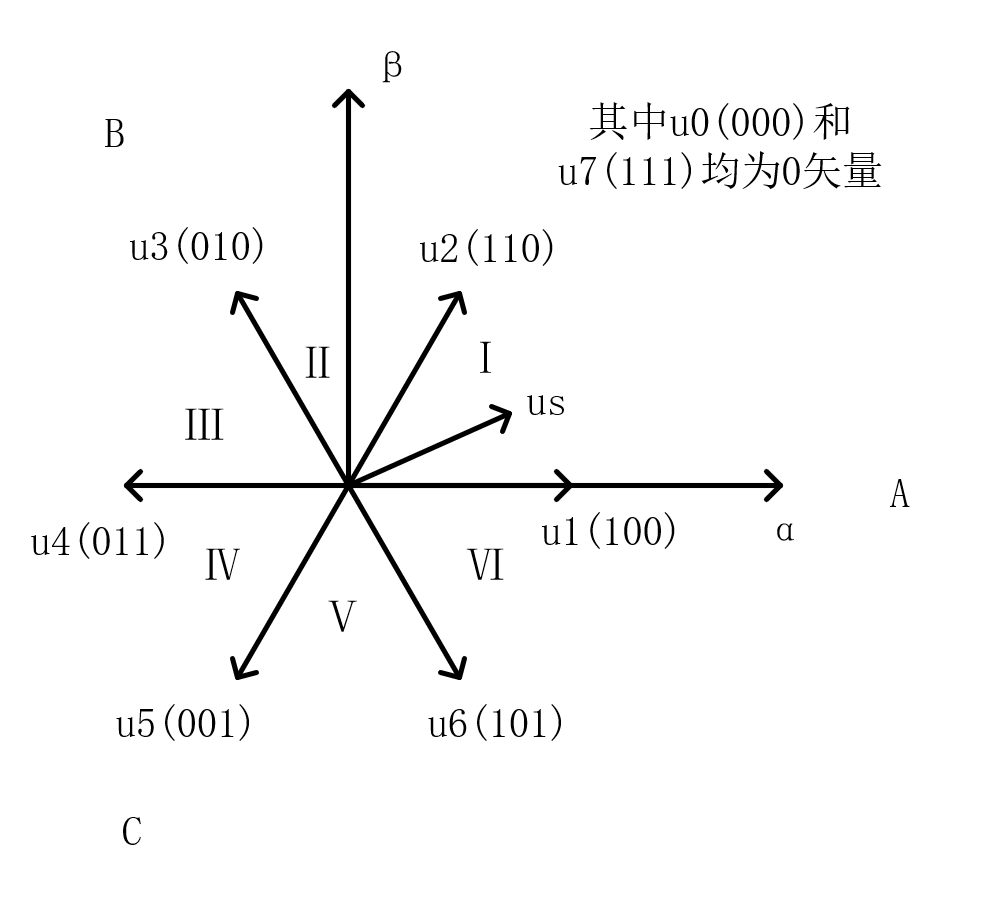
矢量的合成应该遵循相邻原则和平均值等效原则。设这六个区分别为$Ⅰ ~ Ⅵ$，假设现在目标电压矢量处在$Ⅰ$区，那么应该由基本电压矢量$u_1和u_2$合成。如果设开关周期时间为$T_0$，$u_1$作用时间为$t_1$，$u_2$作用时间为$t_2$，那么应该有

$$
T_0u_s=t_1u_1+t_2u_2
$$

根据三角形的正弦定理和余弦定理，就可以算出$t_1,t_2$的大小

如果$t_1+t_2<T_0$，多出来的时间就是零矢量的作用时间，$t_0=T_0-t_1-t_2$

如果$t_1+t_2>T_0$，则令$t_1’=\frac{t_1}{t_1+t_2}T_0,t_2’=\frac{t_2}{t_1+t_2}T_0$

用上述$t_1’,t_2’$代替原有的导通时间

但是$t_1,t_2,t_0$在$T_0$中的时间分配是自由的，一般来说，一方面希望尽量减少开关次数减少开关损耗，另一方面希望减少谐波成分

一般而言有两种实现方式，分别是零矢量集中和零矢量分散方式

以上图img2为例，集中和分散分别对应于img3和img4

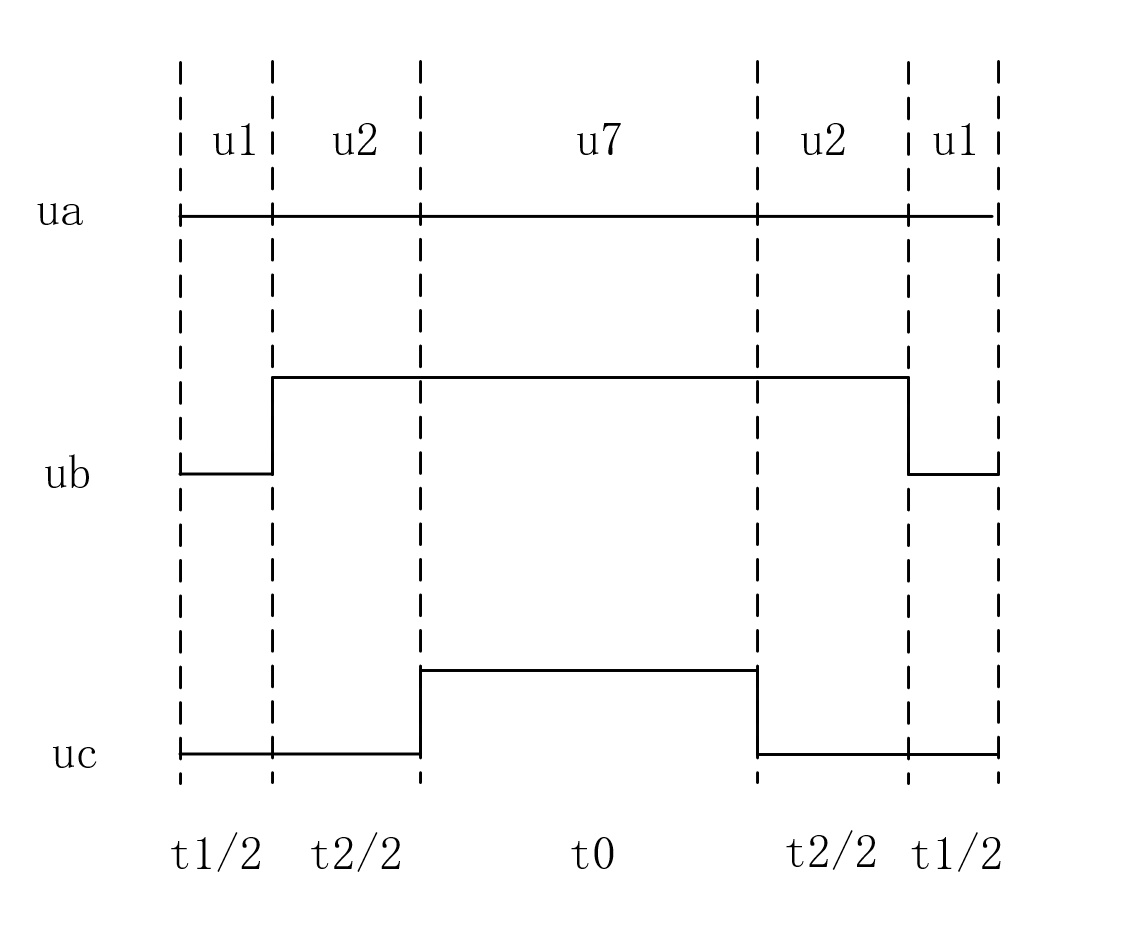
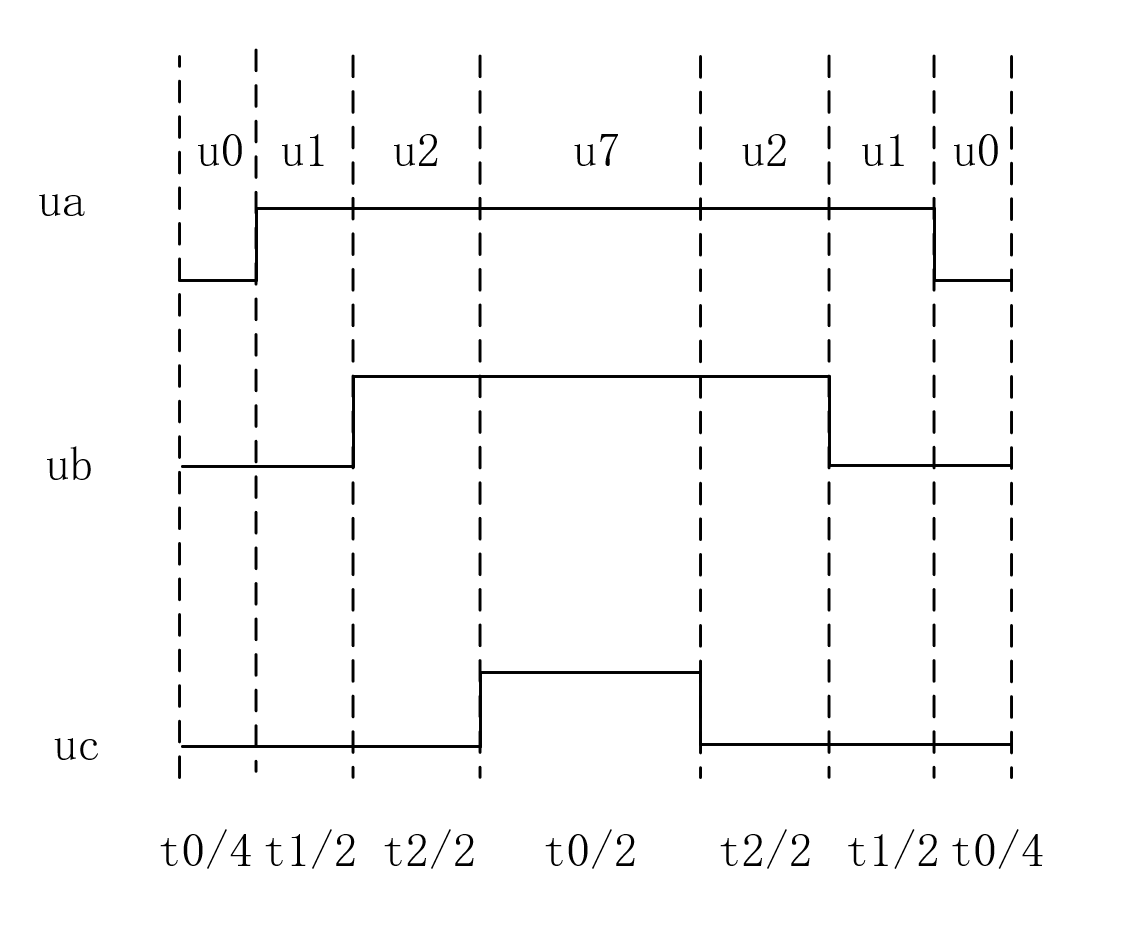
集中的优势在于开关损耗较小，但是由于零矢量单次停留时间过长，会导致谐波成分增加

而分散的优劣势则恰恰与集中相反

Simulink实现

总体的形状应该如img5所示，其中$u_\alpha,u_\beta$给定，也就是说，$u_s$给定，直流电压$U_d$和开关周期时间$T_0$已知

为了实现功能，可以粗略的将整个模块分为三部分：电压矢量区块检测模块、$T_1,T_2$计算模块和PWM波生成模块

电压矢量区块检测模块

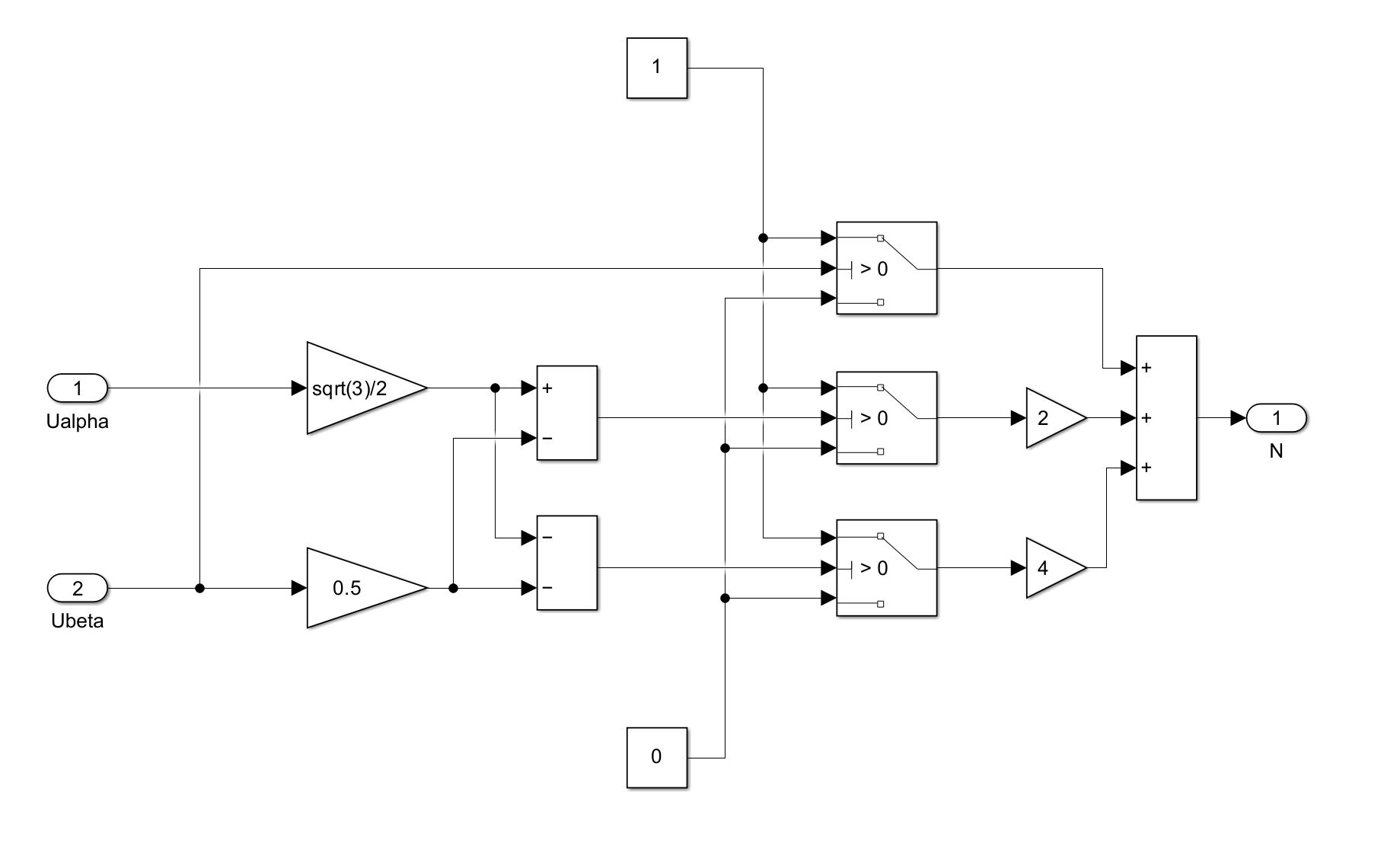
可以用投影的方式确定电压矢量所在区块，如图img6所示，将电压矢量往$1~3$三个方向投影，则可以得到投影大小为

$$
\begin{cases}
u_{ref1}=u_\beta \\
u_{ref2}=\frac{\sqrt{3}}{2}u_\alpha-\frac{1}{2}u_\beta \\
u_{ref3}=-\frac{\sqrt{3}}{2}u_\alpha-\frac{1}{2}u_\beta
\end{cases}
$$

定义一个二进制数$N=CBA_2$,如果$u_{ref1}>0$，则$A=1$，否则$A=0$。其余C对应$u_{ref3}$，B对应$u_{ref2}$，类似定义

那么可以得出

N	3	1	5	4	6	2
扇区	Ⅰ	Ⅱ	Ⅲ	Ⅳ	Ⅴ	Ⅵ

在Simulink当中的实现如img7所示

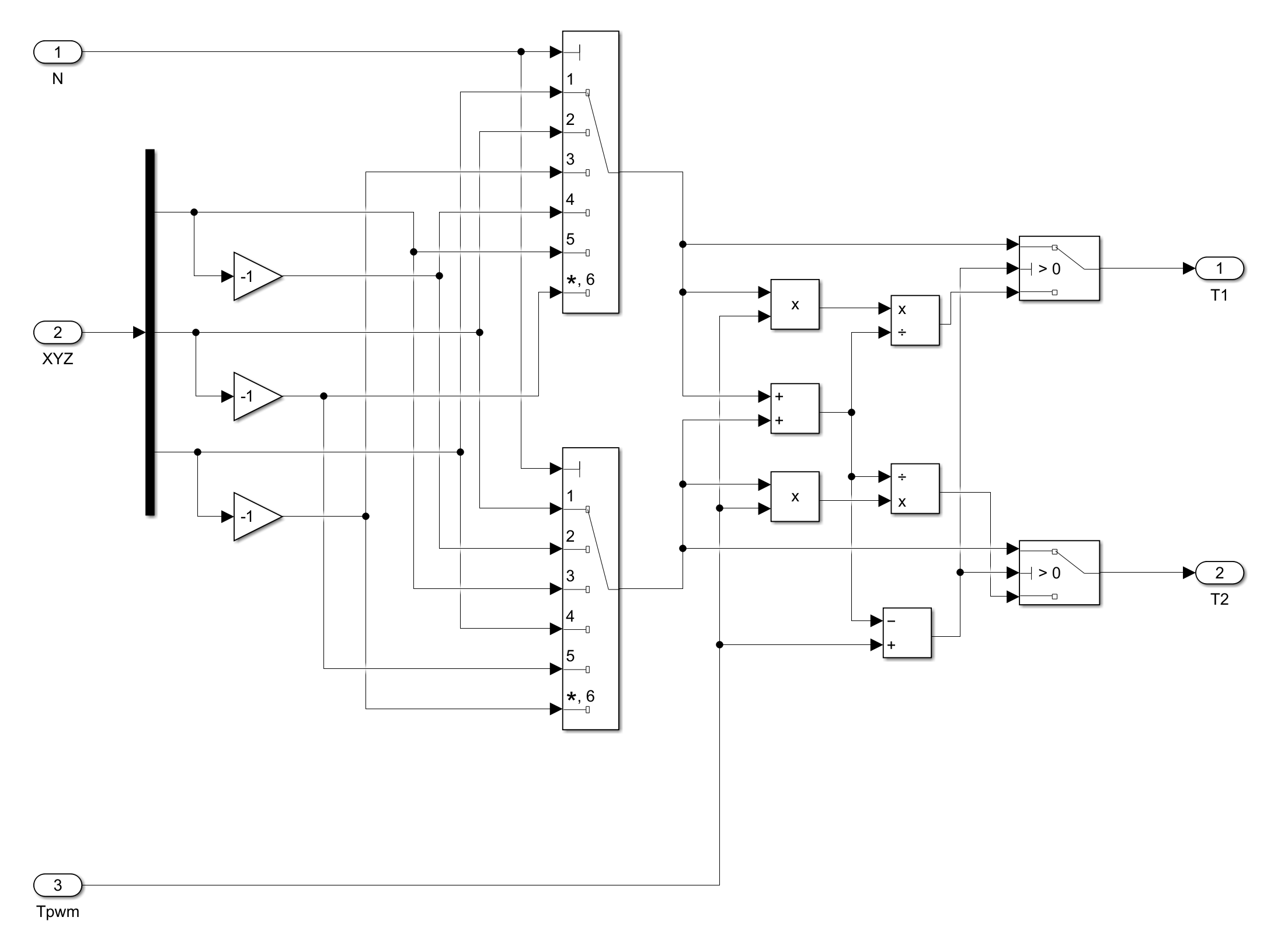
$T_1,T_2$计算模块

以第Ⅰ扇区为例，设$U_{dc}$为直流电压大小，则$|u_1|=|u_2|=…=|u_6|=\frac{2}{3}U_{dc}$

$$
\begin{cases}
u_\beta=\frac{t_2}{T_0}u_2sin\frac{\pi}{3} \\
u_\alpha=\frac{t_2}{T_0}u_2cos\frac{\pi}{3}+\frac{t_1}{T_0}u_1
\end{cases}
$$

于是可得

$$
\begin{cases}
t_1=\frac{\sqrt{3}T_0}{U_{dc}}(\frac{\sqrt{3}}{2}u_\alpha-\frac{1}{2}u_\beta) \\
t_2=\frac{\sqrt{3}T_0}{U_{dc}}u_\beta
\end{cases}
$$

在其他区同理可以计算作用时间

在这里可以对所有情况做一个归纳

定义:

$$
\begin{cases}
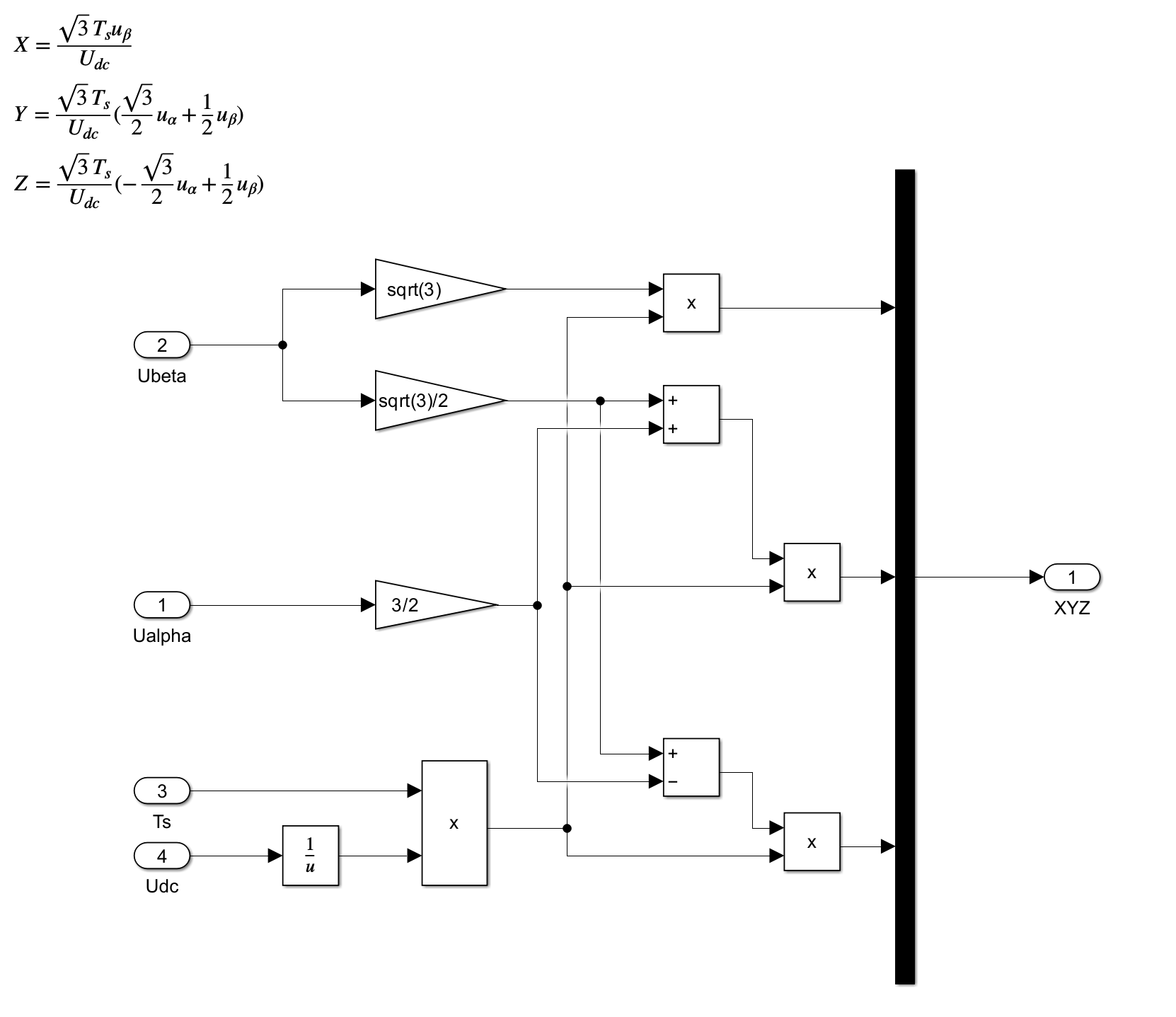
X=\frac{\sqrt{3}T_0}{U_{dc}}u_\beta \\
Y=\frac{\sqrt{3}T_0}{U_{dc}}(\frac{\sqrt{3}}{2}u_\alpha+\frac{1}{2}u_\beta) \\
Z=\frac{\sqrt{3}T_0}{U_{dc}}(-\frac{\sqrt{3}}{2}u_\alpha+\frac{1}{2}u_\beta)
\end{cases}
$$

这样不同N值对应的时间可以总结为下表

N	1	2	3	4	5	6
$T_1$	Z	Y	-Z	-X	X	-Y
$T_2$	Y	-X	X	Z	-Y	-Z

在Simulink当中的实现如img8和img9所示

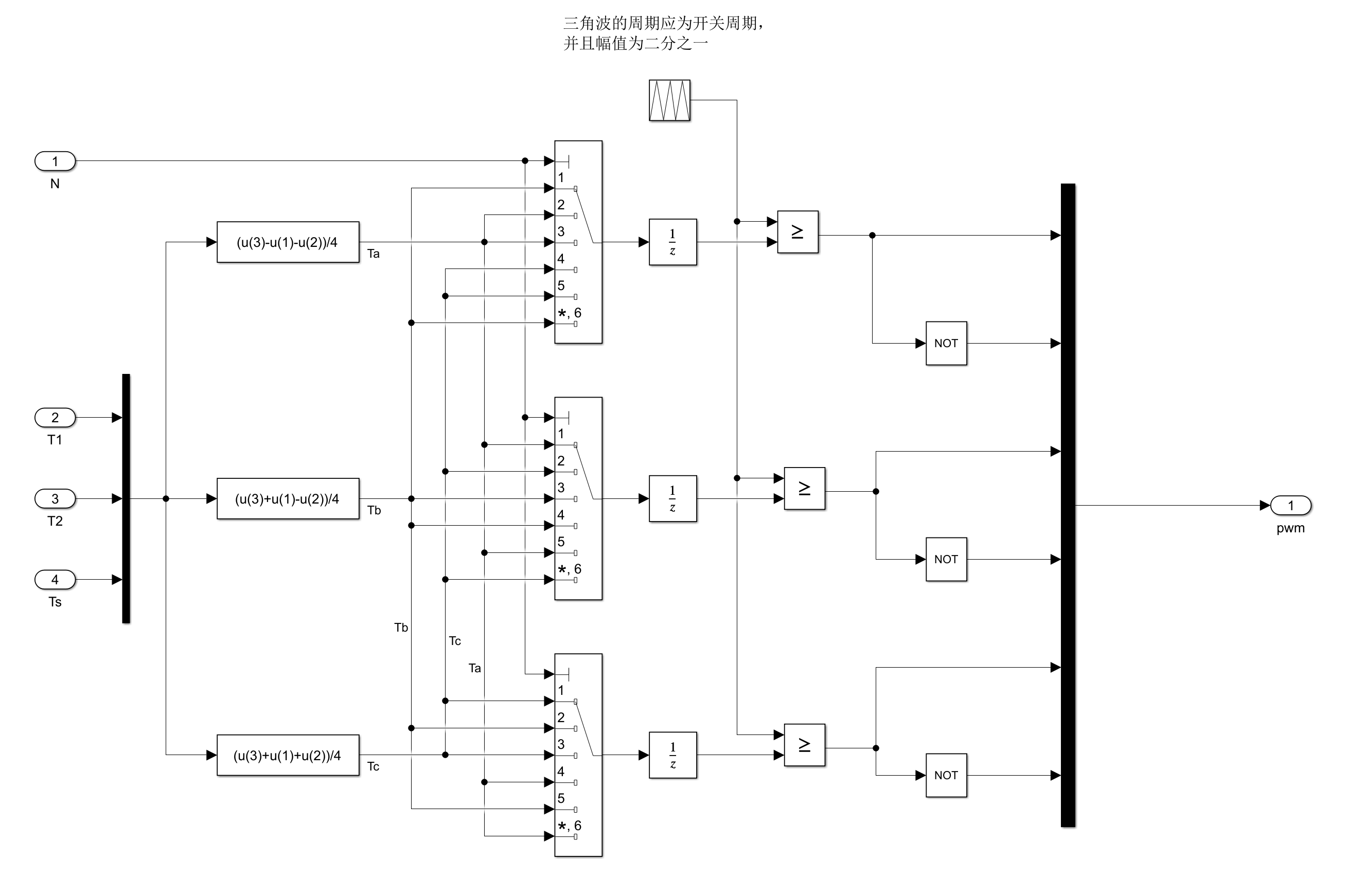
PWM波生成模块

要生成PWM波需要确定$a,b,c$三管的开关时间，下面以第Ⅰ扇区，采用零矢量分散式为例

这里可以参考前面的img4，可以看到三个管的开启时间分别为

$$
\begin{cases}
T_{a1}=\frac{T_0-t_1-t_2}{4} \\
T_{b1}=T_{a1}+\frac{1}{2}t_1 \\
T_{c1}=T_{b1}+\frac{1}{2}t_2
\end{cases}
$$

注：零矢量集中式则可以参考img3推得

对于所有扇区的情况，如果定义$T_a,T_b,T_c$分别为三个管开启的时间，可以将开启时间总结为下表

N	1	2	3	4	5	6
$T_A$	$T_{b1}$	$T_{a1}$	$T_{a1}$	$T_{c1}$	$T_{c1}$	$T_{b1}$
$T_B$	$T_{a1}$	$T_{c1}$	$T_{b1}$	$T_{b1}$	$T_{a1}$	$T_{c1}$
$T_C$	$T_{c1}$	$T_{b1}$	$T_{c1}$	$T_{a1}$	$T_{b1}$	$T_{a1}$

在Simulink当中的实现如img10所示

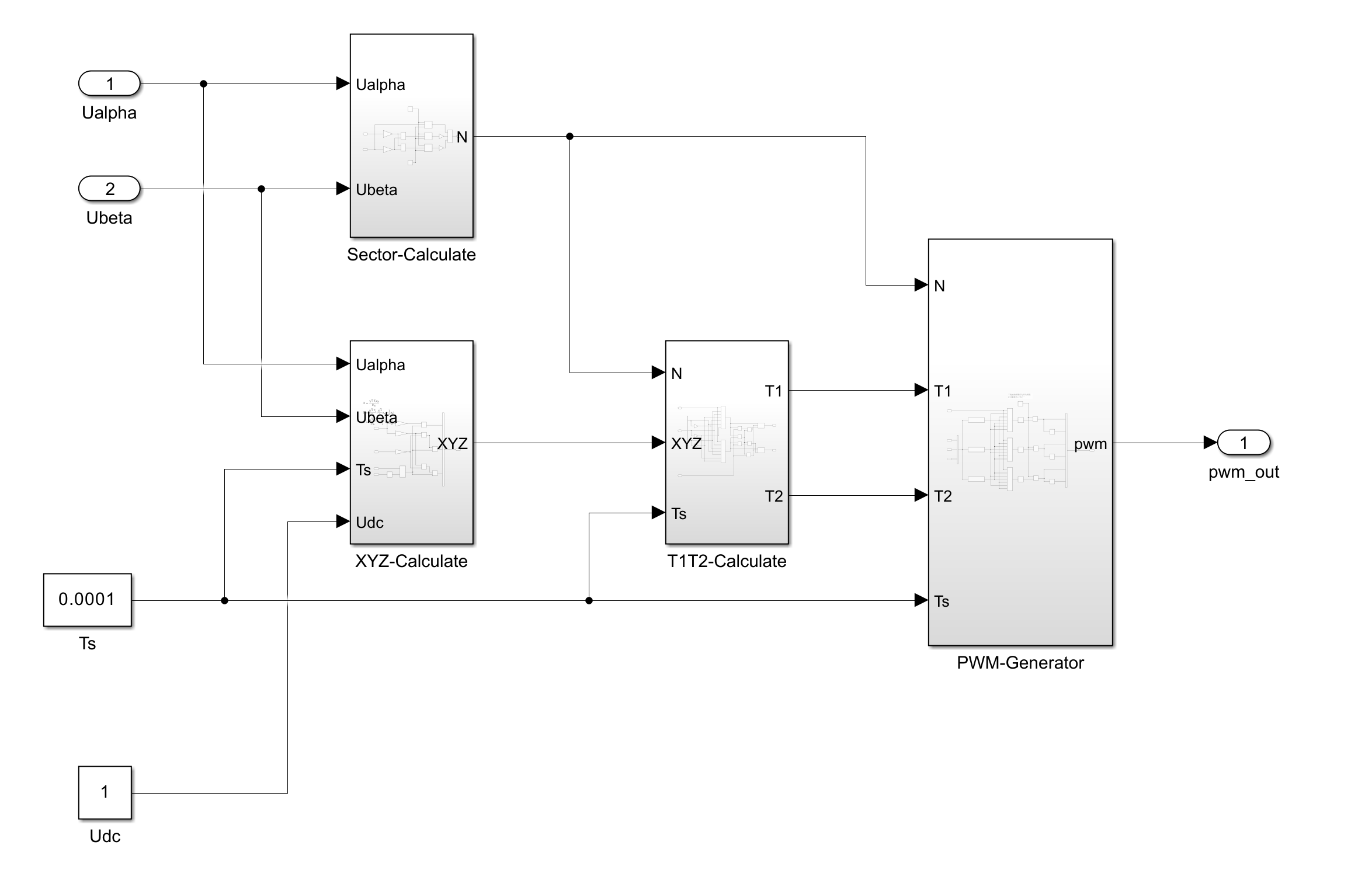
总结

将所有模块联合起来，SVPWM的内部结构就如img11所示

三角接情况

以上论述了电机绕组为星形接法时的情况，那么当绕组为三角形接法时情况会发生什么变化呢？

事实上，基本原理并没有发生变化，只不过基本电压矢量旋转了30°，开关与电压矢量的对应关系发生了改变

后续的电压矢量作用时间计算模块和PWM生成模块按照改变后的关系分别计算即可。