电机建模
电机建模能用来干什么
- 电机建模获得的模型是暂态,当时间足够长之后,电机建模的公式就是电机学中稳态情况下的公式【电机学】
- 拿到电机的参数之后,可以把电机当作传递函数,进行相应的控制【电机控制】
- 将模型输入仿真软件,就可以仿真出电机运行时的各个物理量【仿真算法】
正方向
在建模之前需要先规定正方向:
电磁物理量正方向
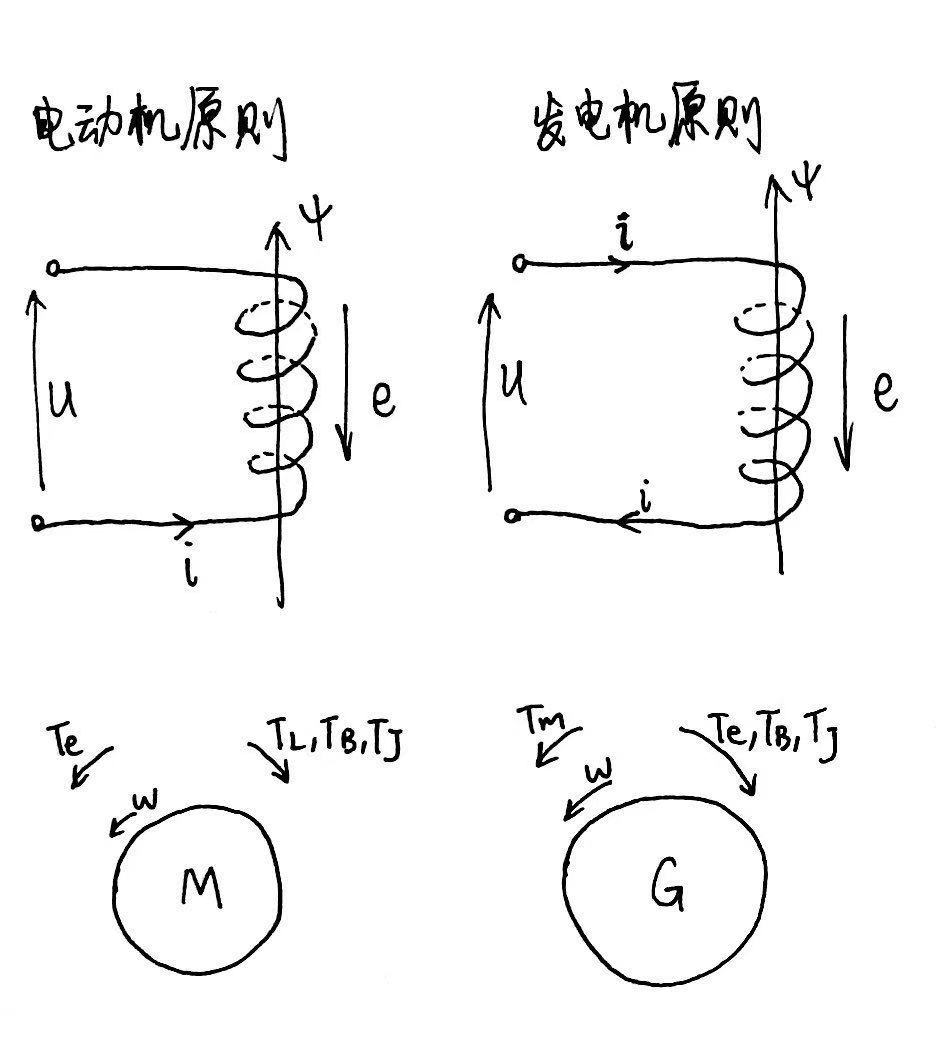
电动机原则
- 磁链 $\psi$ : 磁链的正方向是线圈轴线的正方向
- 电流 $i$ : 正电流产生正磁链
- 电压 $u$ : 与电流为关联参考方向(负载的标法)
- 反电动势 $e$ : 阻碍磁场变化,与电流相反
发电机原则
- 磁链 $\psi$ : 磁链的正方向是线圈轴线的正方向
- 电流 $I$ : 正电流产生负磁链
- 电压 $U$ : 与电流为非关联参考方向(电源的标法)
- 反电动势 $e$ : 阻碍磁场变化,与电流相同
机械物理量正方向
电动机原则
- 电角速度 $\omega$ : 以电枢绕组为参考系,磁场的旋转方向为正方向
- 电磁转矩 $T_{em}$ : 电磁转矩正方向为旋转方向
- 负载转矩 $T_{L}$ , 阻尼转矩 $T_{B}$ , 惯性转矩 $T_{J}$ : 与旋转方向相反
发电机原则
- 电角速度 $\omega$ : 以电枢绕组为参考系,磁场的旋转方向为正方向
- 外施转矩 $T_{m}$ : 电磁转矩正方向为旋转方向
- 电磁转矩 $T_{em}$ , 阻尼转矩 $T_{B}$ , 惯性转矩 $T_{J}$ : 与旋转方向相反
e.g.
方程
方程主要分为电磁方程和机械方程,不同电机整体思路类似,但是细节上有所区分,在这里先介绍几个概念。
海氏算子
定义海氏算子
$$ p=\frac{d}{dt}$$
自感、互感
对于单个线圈而言,方程如下
电动机原则
$$
\begin{cases}
u=e+Ri \\
e=p\psi \\
\psi=Li
\end{cases}
$$
发电机原则
$$
\begin{cases}
u=e-Ri \\
e=p\psi \\
\psi=-Li
\end{cases}
$$
当引入多个线圈后,磁链方程中需要引入互感。方程可能因线圈轴线夹角,线圈正方向原则不同等原因,导致正负号变混乱。
这里规定,当线圈轴线夹角为锐角时互感为正,夹角为钝角时互感为负。而磁链方程按照线圈所使用的原则照写。
e.g.

伪静止线圈
等效后绕组的轴线与构成绕组的实际元件间存在相对运动,则称等效后的线圈为伪静止线圈
如果一个线圈为伪静止线圈,写电磁方程时,需要加上旋转电动势
一般化电机
由于电机之间存在很多共性,有学者提出了一般化电机的概念,希望能够得到一个统一的电机模型。
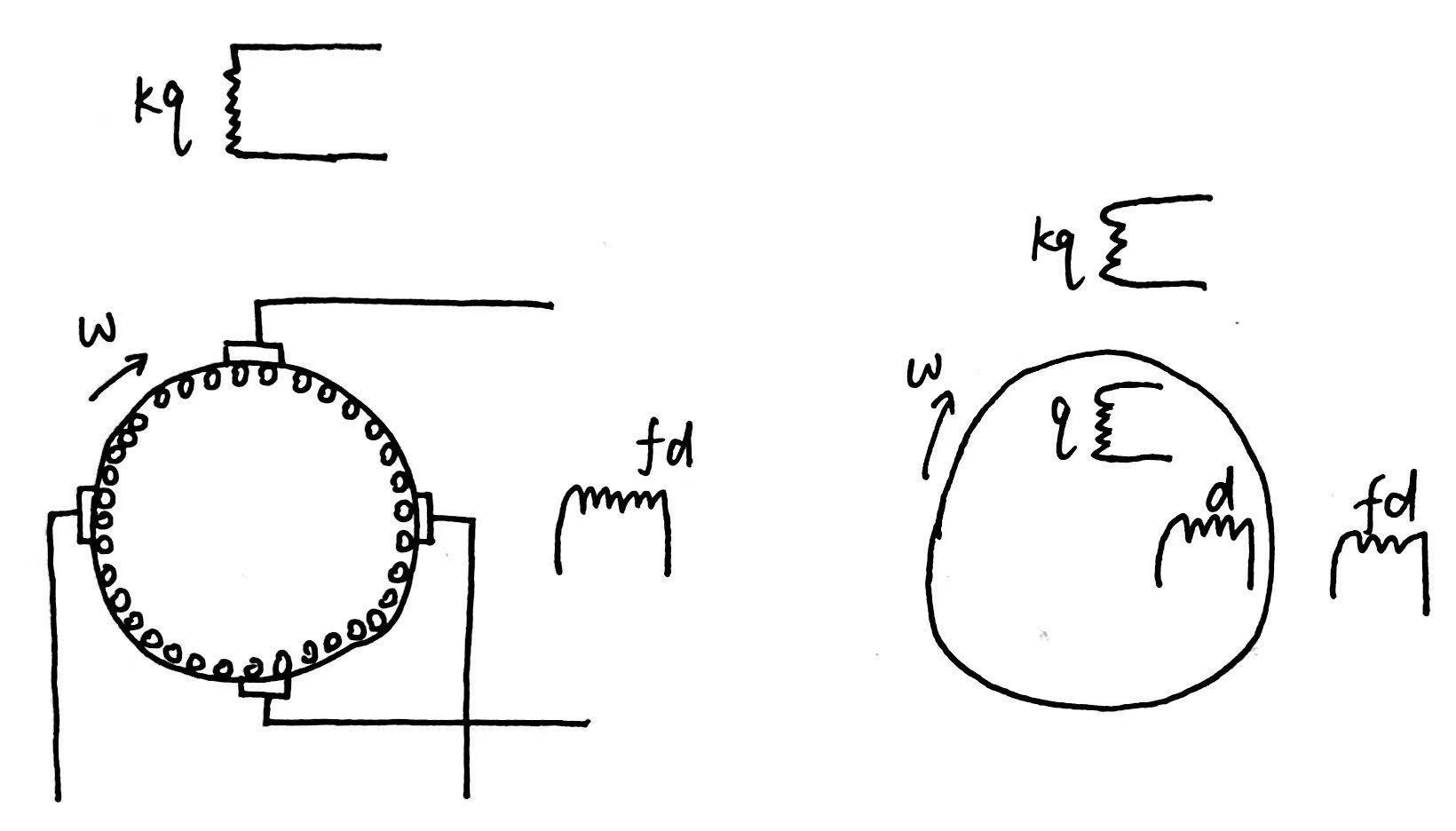
一般化电机的定子绕组由$fd$和$kq$两个线圈构成,转子d轴和q轴上分别有两对电刷,极对数p=1.
不管转子中的绕组是叠绕组、波绕组还是其他什么绕组,如果从d轴和q轴两个端口看,可以将转子绕组等效为$d$和$q$两个线圈。
这是因为绕组的形式只是改变了绕组端部,而槽内的部分产生的反电动势不受影响。
一般化电机示意图如下所示
基本假设
- 磁路不饱和
- 不计剩磁、涡流、磁滞
- 气隙磁密按正弦规律分布
- 电枢漏磁不计
- 正交解耦
电磁方程
假设$fd$和$kq$线圈的正方向按照电动机原则,$d$和$q$线圈按照发电机原则,线圈轴线方向如图所示,则
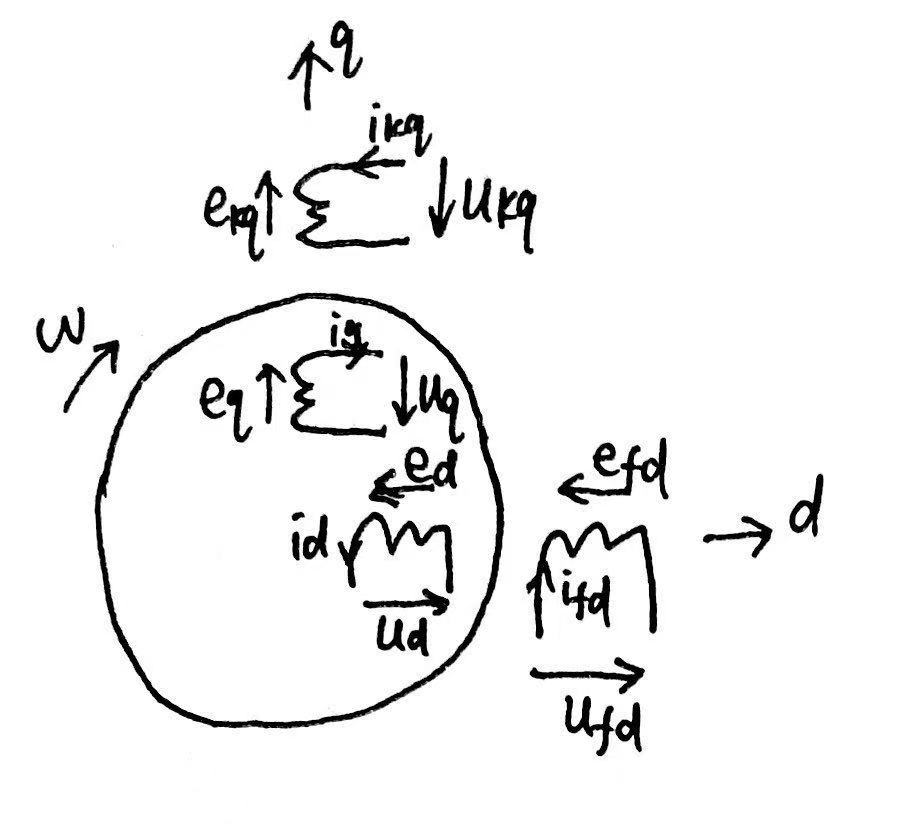
$$
\begin{cases}
u_{kq}=e_{kq}+R_{kq}i_{kq} \\
u_{fd}=e_{fd}+R_{fd}i_{fd} \\
u_{q}=e_q+R_{q}i_{q} \\
u_{d}=e_d+R_{d}i_{d}
\end{cases}
$$
由于u和i都是可以测量得到的量,就不需要继续化简了,接下来需要推导e的表达式
由于$kq$和$fd$线圈没有经过复杂的等效,可以得到,$e_{kq}=p\psi_{kq},e_{fd}=p\psi_{fd}$
$d$和$q$线圈的情况稍微需要推导一下,这里只推导$d$线圈的公式,$q$线圈的公式可以类似得到
由于q轴加不加电刷不影响从d轴电刷看进去的反电动势,故省略了q轴上的电刷
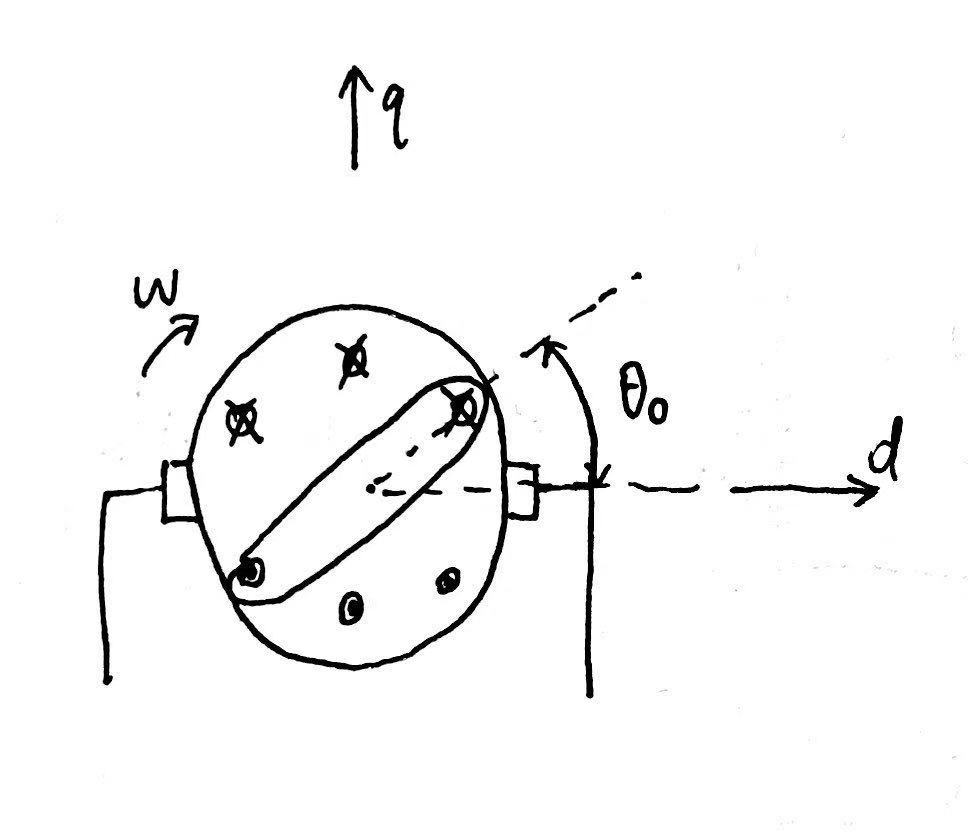
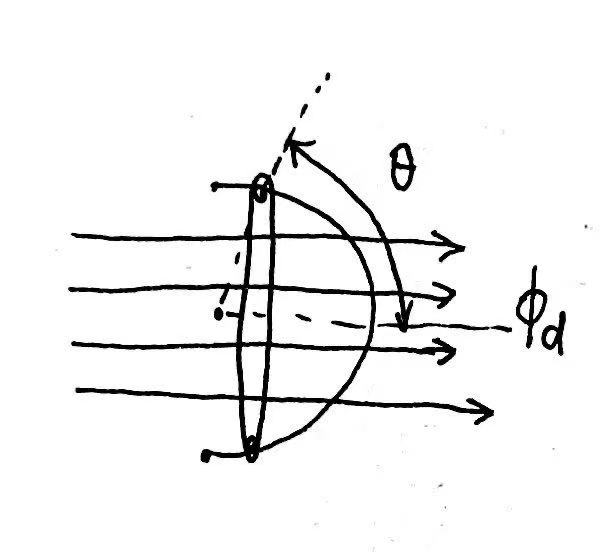
由于之前假设了【气隙磁密按正弦规律分布】,假设$B_d=B_{md}\cos\theta,B_q=B_{mq}\sin\theta$
由于【磁路不饱和】,磁场线性叠加,先分析d轴方向磁场的作用,q轴类似
对于角度为$\theta_0$的线圈,由于流入此线圈的磁通和流出被此线圈分割后的右半圆的磁通相等,有
$$
\phi_0=\int_{\theta_0-\pi}^{\theta_0} {B_dlr} {d\theta}=2B_{md}lr\sin\theta_0
$$
设单位弧度下导体数为$z$,则有
$$
de=z\frac{d\phi_0}{dt}d\theta_0=(2lr\sin\theta_0\frac{dB_{md}}{dt}+2lrB_{md}\cos\theta_0\frac{d\theta_0}{dt})
$$
由于$\frac{d\theta_0}{dt}=-\omega$,
$$
de=z\frac{d\phi_0}{dt}d\theta_0=(2lr\sin\theta_0\frac{dB_{md}}{dt}-2lrB_{md}\cos\theta_0\omega)zd\theta_0
$$
由于cos是偶函数,当e从0积到$\pi$时,第二项应为0,故
$$
e_{dt}’=\int_0^\pi {de}=4lrz\frac{dB_{md}}{dt}
$$
考虑q轴磁场作用,类似的有
$$
e_{dr}’=-4lrzB_{mq}\omega
$$
这里t代表transformer,是变压器电势,也为感生电动势,r代表rotational,是旋转电动势。从这里可以看出,d轴磁场只产生感生电动势,q轴磁场只产生旋转电动势。
由于并联支路数为2,所以从电刷往里看的反电动势应为上述的一半,故
$$e_{dt}=2lrz\frac{dB_{md}}{dt}$$
$$e_{dr}=-2lrzB_{mq}\omega$$
若计算d轴和q轴磁通,可以发现,
$$\phi_d=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} {B_dlr} {d\theta}=2B_{md}lr$$
$$\phi_q=\int_0^\pi{B_qlr}{d\theta}=2B_{mq}lr$$
于是,进一步有
$$e_{dt}=z\frac{d\phi_d}{dt}$$
$$e_{dr}=-z\phi_q\omega$$
若计算d轴和q轴的磁链,又可以发现,
$$\psi_d=\int_{0}^{\frac{\pi}{2}} {2zB_{dm}lr\sin\theta} {d\theta}=z\phi_d$$
$$\psi_q=\int_{0}^{\frac{\pi}{2}} {2zB_{qm}lr\cos\theta} {d\theta}=z\phi_q$$
所以,
$$e_{dt}=p\psi_d$$
$$e_{dr}=-\psi_q\omega$$
$$e_d=e_{dt}+e_{dr}=p\psi_d-\psi_q\omega$$
对于$q$线圈,同样的方法,只需要更改一下积分上下限,就可以得到
$$e_{qt}=p\psi_q$$
$$e_{qr}=\psi_d\omega$$
$$e_q=e_{qt}+e_{qr}=p\psi_q+\psi_d\omega$$
总结一下方程有
$$
\begin{cases}
u_d=p\psi_d-\omega\psi_q-R_di_d \\
u_q=p\psi_q+\omega\psi_d-R_qi_q \\
u_{fd}=p\psi_{fd}+R_{fd}i_{fd} \\
u_{kq}=p\psi_{kq}+R_{kq}i_{kq}
\end{cases}
$$
但是这个时候的表达式中的$\Psi_d$和$\Psi_q$还不是端口能够测量得到的变量,因此还需要进一步变形
由于【正交解耦】,可得
$$
\begin{cases}
\psi_d=-L_di_d+M_{afd}i_{fd} \\
\psi_q=-L_qi_q+M_{akq}i_{kq} \\
\psi_{fd}=L_{fd}i_{fd}-M_{fad}i_d \\
\psi_{kq}=L_{kq}i_{kq}-M_{kaq}i_q
\end{cases}
$$
至此,电磁状态方程已经推导完毕,我们可以用矩阵的形式使其表达起来更加简洁,设
$$
U=
\begin{bmatrix}
u_d \\
u_q \\
u_{fd} \\
u_{kq}
\end{bmatrix},R=
\begin{bmatrix}
-R_d & 0 & 0 & 0 \\
0 & -R_q & 0 & 0 \\
0 & 0 & R_{fd} & 0 \\
0 & 0 & 0 & R_{kq}
\end{bmatrix},I=
\begin{bmatrix}
i_d \\
i_q \\
i_{fd} \\
i_{kq}
\end{bmatrix}
$$
$$
L=
\begin{bmatrix}
-L_d & 0 & M_{afd} & 0 \\
0 & -L_q & 0 & M_{akq} \\
-M_{fad} & 0 & L_{fd} & 0 \\
0 & -M_{kaq} & 0 & L_{kq}
\end{bmatrix},G=
\begin{bmatrix}
0 & L_q & 0 & -M_{akq} \\
-L_d & 0 & M_{afd} & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
$$
则有
$$
U=(R+Lp+\omega G)I
$$
这里可以看到,等效的绕组线圈出现了旋转电动势这一项
不失一般性的,当被等效的绕组为【伪静止线圈】时,会多出这一项
机械方程
按照发电机原则规定正方向
转矩方程$$T_m=T_e+T_D+T_J$$
在这条方程中,$T_m$是可以控制的外部变量,$T_D=B\omega,T_J=Jp\omega$,因此需要获得$T_e$的表达式
为获得$T_e$可以使用能量守恒定律或者虚位移法等方法
能量守恒定律推导$T_e$
能量守恒$$电磁输入功率P_{dq}+机械输入功率P_m=电磁储能功率+机械储能功率+电磁损耗+机械损耗$$
根据规定的正方向,$$P_{dq}=-u_di_d-u_qi_q+u_{fd}i_{fd}+u{kq}i_{kq}$$
设,
$$
U’=
\begin{bmatrix}
-u_d \\
-u_q \\
u_{fd} \\
u_{kq}
\end{bmatrix},R’=
\begin{bmatrix}
R_d & 0 & 0 & 0 \\
0 & R_q & 0 & 0 \\
0 & 0 & R_{fd} & 0 \\
0 & 0 & 0 & R_{kq}
\end{bmatrix}
$$
$$
L’=
\begin{bmatrix}
L_d & 0 & -M_{afd} & 0 \\
0 & L_q & 0 & -M_{akq} \\
-M_{fad} & 0 & L_{fd} & 0 \\
0 & -M_{kaq} & 0 & L_{kq}
\end{bmatrix},G’=
\begin{bmatrix}
0 & -L_q & 0 & M_{akq} \\
L_d & 0 & -M_{afd} & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
$$
则有
$$
\begin{split}
P_{dq}&=U’^TI=((R’+L’p+\omega G’)I)^TI \\
&= I^T(R’^T+L’^Tp+\omega G’^T)I \\
&=I^TRI+I^TL’^TpI+I^T\omega G’^TI
\end{split}
$$
$$
P_m=\omega T_m=\omega(T_e+T_D+T_J)
$$
而对于等式右边有
$$电磁储能功率=I^TL’pI$$
$$机械储能功率=\omega T_J$$
$$电磁损耗=I^TR’I$$
$$机械损耗=\omega T_D$$
因此,
$$\omega I^TG’I+\omega T_e=0$$
所以,
$$
\begin{split}
T_e&=-I^TG’I \\
&=-
\begin{bmatrix}
i_d \\
i_q \\
i_{fd} \\
i_{kq} \\
\end{bmatrix}^T
\begin{bmatrix}
0 & -L_q & 0 & -M_{akq} \\
L_d & 0 & -M_{afd} & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0
\end{bmatrix}
\begin{bmatrix}
i_d \\
i_q \\
i_{fd} \\
i_{kq} \\
\end{bmatrix} \\
&=-
\begin{bmatrix}
i_d \\
i_q \\
i_{fd} \\
i_{kq} \\
\end{bmatrix}^T
\begin{bmatrix}
\psi_q \\
-\psi_d \\
0 \\
0
\end{bmatrix}=\psi_d i_q-\psi_q i_d=\frac{1}{\omega}(e_{qr}i_q+e_{dr}i_d)
\end{split}
$$
综上,将电磁转矩的表达式代入转矩方程中,可得
$$p\omega=\frac{T_m-(\psi_d i_q-\psi_q i_d)-B\omega}{J}$$
总结
这样一来,电磁方程和机械方程都有了,可以看到这两个方程当中互有另一个方程的状态变量,因此是耦合的
拿到模型后,可以参考电机建模能用来干什么
本章当中仅仅涉及了一般化电机的内容,对于直流电机、异步电机、同步电机,实际上可以通过坐标变换进行转化,后续有机会将继续讨论